Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Понятия и факты римановой геометрии

См. предыдущие разделы:
Понятие о римановой геометрии
Определение риманова пространства

1) Касательное евклидово пространство

По самому определению римановой геометрии, метрика риманова пространства в окрестности каждой точки совпадает (с точностью до бесконечно малых выше 1-го порядка) с евклидовой метрикой. Это позволяет сопоставить с каждой точкой A данного риманова пространства R так называемое касательное евклидово пространство - евклидово пространство E_A, в которое отображается какая-то окрестность U точки A так, что относительное искажение расстояний стремится к нулю при приближении к точке A. Аналитически это сводится к следующему: вблизи некоторой точки A₀ пространства E_A вводятся координаты так, что в них квадрат линейного элемента ds₀² евклидова пространства E_A выражается в точке A₀ такой же формой Σ_i,j(A)g_i,jdx_idx_j какой выражается квадрат линейного элемента риманова пространства R в точке A. Значение понятия касательного евклидова пространства состоит в том, что, поскольку можно пренебречь малыми выше первого порядка, окрестность точки в римановом пространстве можно заменять областью касательного пространства.

2) Длина дуги s

Длина дуги s кривой x_i = x_i(t) (i = 1, 2, ..., n, t₁≤t≤t₂) в римановом пространстве R определяется как интеграл

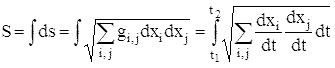
вдоль этой кривой. Если любые две точки пространства R соединимы кривой, то R становится метрическим пространством: расстояние ρ(X, Y) между двумя точками определяется как точная нижняя грань длин кривых, соединяющих эти точки, и называется внутренней метрикой риманова пространства R.

3) Угол между двумя кривыми

Угол между двумя исходящими из одной точки A кривыми определяется как угол между касательными векторами к кривым в точке A.

4) Объём n-мерной области

Объём V n-мерной области G риманова пространства определяется по формуле

5) Геодезические

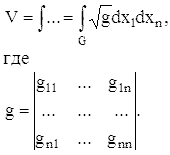
Линии, которые на достаточно малых участках являются кратчайшими из всех кривых с теми же концами, называются геодезическими, они играют роль прямых в римановом пространстве R. По определению, они являются экстремалями функционала

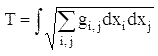
и удовлетворяют уравнению

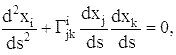
где Γ_jkⁱ - так называемые символы Кристоффеля, выражающиеся через компоненты метрического тензора g_ij и их первые производные. Через каждую точку риманова пространства в любом направлении проходит геодезическая, и притом единственная.

6) Подпространства

m-мерное подмногообразие (поверхность) риманова пространства задаётся параметрическими уравнениями x_i = x_i(u₁, u_m), где u = 1, ..., n; предполагается, что матрица имеет ранг m. Длины кривых на таком подмногообразии выражаются посредством линейного элемента

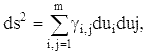
ввиду чего каждое такое подмногообразие можно рассматривать как m-мерное риманово пространство (оно называется m-мерным подпространством исходного риманова пространства). Этим, в частности, решается вопрос о вычислении объёмов (площадей) m-мерных областей риманова пространства.

7) Основная теорема римановой геометрии

По определению, всякое риманово пространство в бесконечно малом совпадает с евклидовым с точностью до малых выше 1-го порядка (относительно дифференциалов координат). Однако оказывается, что между римановым пространством R и касательным к нему евклидовым пространством в окрестности U_A некоторой точки A можно установить такое соответствие, при котором оба пространства будут совпадать с точностью до малых выше 2-го порядка. Для этого проводят из точки A геодезические во всех направлениях и каждой из них в касательном пространстве E_A сопоставляют луч соответствующего направления, а затем устанавливают такое соответствие этих лучей и геодезических, при котором длины дуг геодезических и соответствующих им лучей равны. В достаточно малой окрестности точки A такое соответствие будет взаимно однозначным; оно и является искомым. А именно, если ввести в касательном пространстве декартовы координаты x₁, ..., x_n и приписать их значения соответствующим точкам окрестности U_A, то между линейными элементами ds риманова и ds₀ евклидова пространств будет такая связь:
 

Читать дальше:
Приложения и обобщения римановой геометрии

Опубликовано по материалам: Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков и др. - М.: Сов. энциклопедия, 1988. - 847 с. стр. 530 - 531.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)