Переход на главную страницу сайта “Термист” Термист
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
Главная О сайте Стандарты Технология Устройства
Лаборатория Библиотека Глоссарий Желтые страницы Обратная связь

Распределение вероятностей

 

Распределение вероятностей - одно из центральных понятий теории вероятностей и математической статистики. Определение распределения вероятностей равносильно заданию вероятностей всех случайных событий, описывающих некоторое случайное явление. Распределение вероятностей какой-либо действительной случайной величины x, возможные значения x1, x2, ..., xn, ... которой образуют конечную или бесконечную последовательность, задается указанием этих значений и соответствующих им вероятностей P{x = xn}: p1, p2, ..., pn, ... (pn должны быть положительными и в сумме составлять единицу).

Так, например, для числа очков, выпадающих на верхней грани при подбрасывании игральной кости, распределение вероятностей задастся таблицей:

Возможные значения xn 1 2 3 4 5 6
Соответствующие вероятности pn 1/6 1/6 1/6 1/6 1/6 1/6

Распределения вероятностей указанного типа называются дискретными. Примерами дискретных распределений вероятностей служат:

биномиальное распределение, определяемое вероятностями
Биномиальное распределение
где n>0 - целое, 0<p<1;

распределение Пуассона, определяемое вероятностями

где λ>0;

геометрическое распределение;

распределение Паскаля.

Во многих случаях задание распределения вероятностей указанием возможных значений случайной величины и соответствующих им вероятностей невозможно. Например, если случайная величина принимает любые значения из отрезка [-1/2, 1/2], то распределение вероятностей задаётся указанием вероятностей того, что случайная величина примет значение из любого заданного интервала, принадлежащей отрезку [-1/2, 1/2], т.к. вероятность каждого отдельного значения может быть равна нулю. Если существует такая функция p(x), что вероятность попадания x в любой интервал (a, b) на прямой равна
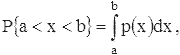
Вероятность попадания случайной величины x в интервал (a, b)
причем
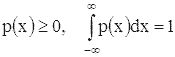Свойства плотности распределения,
то распределение вероятностей величины x называют абсолютно непрерывным, а функция p(x) носит название плотности вероятности.

В случае равномерного распределения на отрезке [-1/2, 1/2]
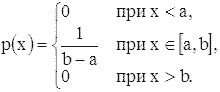
Вероятность для равномерного распределения

Важнейшее распределение вероятностей непрерывного типа - нормальное распределение с плотностью
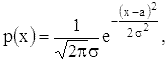
Нормальное распределение случайной величины
где -∞ < a < ∞ и σ > 0.

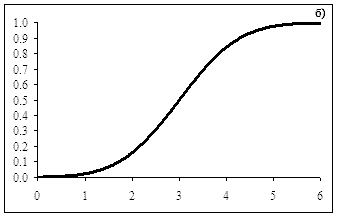Плотность нормального распределения Интегральная функция нормального распределения

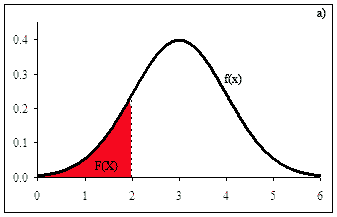
Нормальное распределение со средним a = 3 и среднеквадратичным отклонением σ = 1.
а) плотность вероятности p(x) для рассматриваемого нормального распределения;
б) интегральная функция распределения F(x) = P(X < x).

На рис. а) выделена область соответствующая F(2) = P(X < 2). Эта область показывает вероятность того, что случайная величина X окажется меньше 2.

См. также:

распределение Коши;

Распределение Максвелла;

распределение Пирсона;

показательное распределение;

распределение Релея;

распределение Стьюдента;

χ2-распределение.

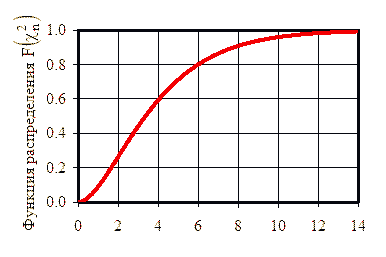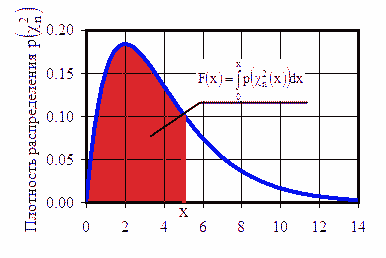
Плотность χ2-распределения при степени свободы n = 4 и функция распределения

Распределения вероятностей не исчерпываются дискретными и непрерывными типами. Они могут быть и более сложной природы. Описание распределения вероятностей, пригодное во всех случаях, может быть, например, достигнуто при помощи функции распределения, которая для любой случайной величины X при каждом действительном x определяется формулой
F(x) = P{X < x}.

Функция распределения F(x) монотонно неубывающая, непрерывная слева и такая, что
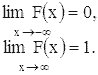
Свойства функции распределения

Вероятность того, что x примет значение из некоторого интервала [a, b) на прямой равна
P{a ≤ x < b} = F(b) - F(a).
Функция распределения однозначно задаёт соответствующее распределение вероятностей случайной величины.

Часто полное описание распределения вероятностей (например, при помощи плотности распределения p(x) или функции распределения F(x)) заменяют заданием небольшого числа числовых характеристик, которые указывают, как правило, наиболее типичные (в том или ином отношении) значения случайной величины и степень рассеяния значений случайной величины около некоторого типичного значения. Из этих характеристик наиболее употребительны математическое ожидание (среднее значение) и дисперсия. Для случайной величины x с дискретным p(x) среднее значение xср определяется как
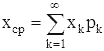Математическое ожидание для дискретной случайной величины,
а для величины x с абсолютно непрерывным p(x) - как
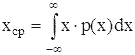
Математическое ожидание для непрерывной случайной величины
при условии, что указанные ряд и интервал сходятся абсолютно.

Дисперсия x по определению равна
Dx = ((x-xср)2)ср.

О других числовых характеристиках распределения вероятностей см. "Вероятное отклонение", "Квадратичное отклонение", "Квантиль", "Медиана", "Мода", "Момент".

Если случайные величины x и y связаны соотношением y = f(x), где f(x) - заданная функция, то p(y) может быть выражено через p(x). Например, если x имеет нормальное распределение с параметрами a и σ2, то y = ex имеет так называемое логарифмически нормальное распределение с плотностью
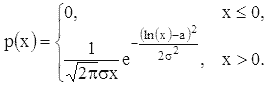
Плотность логарифмически нормального распределения

Если y является линейной функцией от x, то есть, если y = ax + b, то при a > 0
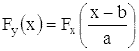Функция распределения при линейной зависимости,
и в абсолютно непрерывном случае
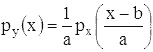Плотность распределения при линейной зависимости.

Помимо функций распределения полную информацию о распределении вероятностей содержат так называемые производящие функции и характеристические функции.

Производящая функция распределения вероятностей случайной величины x с целыми неотрицательными значениями определяется формулой
φ(t) = Ezx
при каждом фиксированном z, |z| ≤ 1.

Характеристическая функция распределения вероятностей произвольной случайной величины x определяется по формуле
f(x) = Eeitx
для любого действительного t, -∞ < t < ∞.

Производящие и характеристические функции однозначно определяют соответствующие распределения вероятностей.

Если x1, x2, ..., xn - несколько случайных величин, определенных на одном и том же вероятностном пространстве, то говорят о совместном распределении вероятностей величин x1, x2, ..., xn или о распределении вероятностей случайного вектора x = (x1, x2, ..., xn) - многомерном распределении вероятностей. Многомерное распределение вероятностей задаётся набором вероятностей вида P{X1 = x1, X2 = x2, ..., Xn = xn} (дискретный тип) или с помощью плотности p(x1, x2, ..., xn) (непрерывный тип) или же в общем случае функцией распределения F(x1, x2, ..., xn). Если случайные величины x1, x2, ..., xn независимы, то распределение вероятностей x = (x1, x2, ..., xn) определяется распределением отдельных величин xk, k = 1, 2, ..., n. В ином случае приходится рассматривать условные распределения вероятностей одних величин при фиксированных значениях других и соответствующие числовые характеристики (условные математические ожидания, условные дисперсии, смешанные моменты). О многомерных распределениях вероятностей см. также "Корреляция", "Регрессия".

Особое внимание в теории вероятностей уделяется точным и асимптотическим распределениям вероятностей сумм случайных величин. Например, распределение вероятностей суммы двух независимых случайных величин x и y, которые имеют распределения с плотностями pX(x) и pY(x), задается плотностью
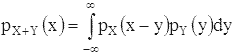(формула свертки).

Однако для вычисления распределения вероятности сумм при большом числе слагаемых явные формулы свертки практически непригодны, а используются производящие и характеристические функции, так как эти функции при сложении независимых случайных величин перемножаются. Проблемы сходимости распределения вероятностей, в частности распределения вероятностей сумм независимых случайных величин при неограниченном увеличении числа слагаемых, изучается предельными теоремами теории вероятностей. О сходимости биномиального распределения к распределению Пуассона см. "теорему Пуассона", о сходимости к нормальному распределению см. "теорему Лапласа" и "теорему Ляпунова".

Важное значение имеют предельные теоремы о распределении вероятностей в математической статистике. Статистическим аналогом распределения вероятностей служит так называемое эмпирическое распределение. Пусть x1, x2, ..., xn - результаты наблюдений, которые предполагаются независимыми, одинаково распределёнными случайными величинами с функцией распределения вероятностей F(x). Эмпирическое распределение вероятностей характеризуется так называемой эмпирической функцией распределения
F*n(x) = nx/n,
где nx - число наблюдений с Xk < x, которой соответствует так называемое выборочное среднее
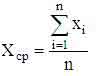
Оценка среднего значения исходного ряда
и выборочная дисперсия
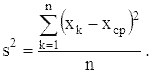
Оценка дисперсии

Эмпирическое распределение и его характеристики используются для приближенного представления теоретического распределения вероятностей и его характеристик, см. "Математическая статистика", "Непараметрические методы математической статистики", "Статистическая оценка".

Распределение вероятностей объектов, более общих, чем случайные величины и случайные векторы (см., например, "Случайный элемент"), определяется в рамках понятия вероятностного пространства как общей математической модели случайного явления. Об этом общем подходе к распределению вероятностей на основе теории меры и об аксиоматическом определении распределения вероятностей см. "Теория вероятностей".

 

Опубликовано по материалам: Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков и др. - М.: Сов. энциклопедия, 1988. - 847 с. стр. 518 - 519.

 

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)