
Термомеханическое упрочнение арматурного проката
технология, средства, разработка
 |
Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка |
| Главная | О сайте | Стандарты | Технология | Устройства |
| Лаборатория | Библиотека | Глоссарий | Желтые страницы | Обратная связь |
Постановка задачи
 Выходя
из начала координат 0, частица с равной вероятностью сдвигается на один шаг либо
на юг, либо на север, и одновременно (и тоже с равной вероятностью) на один шаг
либо на восток, либо на запад. После того как шаг сделан, движение продолжается
аналогичным образом из нового положения и так далее до бесконечности
(рис. 51.1). Какова вероятность того, что частица когда-нибудь вернется в начало
координат?
Выходя
из начала координат 0, частица с равной вероятностью сдвигается на один шаг либо
на юг, либо на север, и одновременно (и тоже с равной вероятностью) на один шаг
либо на восток, либо на запад. После того как шаг сделан, движение продолжается
аналогичным образом из нового положения и так далее до бесконечности
(рис. 51.1). Какова вероятность того, что частица когда-нибудь вернется в начало
координат?
Решение задачи
 |
|
|
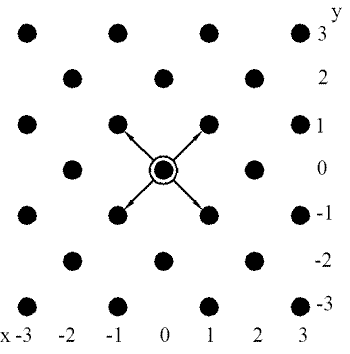
Рис. 51.1. Часть решетки из точек, проходимых частицей в задаче о двумерном случайном блуждании. На каждом шаге частица сдвигается из данного положения на северо-восток, северо-запад, юго-восток или юго-запад, причем все эти направления равновероятны. |
В одномерном случайном блуждании
(см. задачу "На
краю утеса") мы нашли, что вероятность возвращения частицы в начало
есть l, если вероятности шагов налево и направо одинаковы. Но положение дел все
же весьма деликатно сбалансировано. Если бы одна из вероятностей отличалась от
1/2, то частица удалилась бы в бесконечность. В случае двух измерений можно
предположить, что у частицы больше возможностей для ухода в бесконечность.
Выясним, так ли это. Мы постараемся найти среднее число возвращений частицы в
начало и отсюда определить значение вероятности возвращения частицы. Прежде
всего, сколько раз частица вернется в начало? Если P есть вероятность
возвращения, то 1 - P = Q есть вероятность того, что возвращения не будет. Тогда
вероятность ровно x возвращений есть PxQ, так как после каждого
возвращения частицу можно рассматривать как снова выходящую из начала. Если бы P
было известно, то среднее число возвращений в начало координат можно было бы
найти, суммируя геометрический ряд вида
![]()
Из задачи "Об испытаниях до первого успеха" видно, что среднее число возвращений есть величина, обратная к вероятности успеха. В упомянутой задаче успех заканчивал серию испытаний, в нашей же задаче серию заканчивает невозвращение в начало, так что среднее число испытаний до первого успеха равно 1/Q. Следовательно, среднее число успехов равно 1/Q - 1. Если Q = l, то среднее число успехов равняется 0, и с вероятностью 1 частица будет потеряна и никогда не вернется. С другой стороны, чем меньше Q, тем больше среднее число возвращений. Действительно, каждому значению Q отвечает среднее число возвращений и для каждого среднего числа найдется соответствующее Q. Если среднее число возвращений перед окончательным уходом бесконечно (неограниченно), то Q должно быть равным нулю, а P равным 1. Более формально, P → 1 при µ → ∞. Теперь видно, что для решения задачи о двумерном блуждании мы должны подсчитать значение µ.
Выходя из начала, частица может попасть в него обратно лишь после четного числа шагов. Более того, ее путь может быть представлен как «произведение» двух независимых одномерных случайных блужданий, каждое из которых начинается в начале координат, и одно происходит в вертикальном направлении, а другое - в горизонтальном направлении. После двух шагов горизонтальная компонента x имеет распределение
| x | -2 | 0 | 2 |
| P(x) | 1/4 | 2/4 | 1/4 |
Вертикальная компонента после двух шагов распределена точно так же, и вероятности их совместного распределения в девяти точках выглядят следующим образом:
| Распределение X | |||||||
| x | -2 | 0 | 2 | ||||
| P(x) | 1/4 | 2/4 | 1/4 | ||||
| Распределение Y | |||||||
| y | P(y) | P(x,y) | |||||
| 2 | 1/4 | 1/16 | 2/16 | 1/16 | |||
| 0 | 2/4 | 2/16 | 4/16 | 2/16 | |||
| -2 | 1/4 | 1/16 | 2/16 | 1/16 | |||
|
Рис. 51.2. Совместное распределение X и Y после двух шагов |
|||||||
Основной факт, на который мы хотим обратить внимание, состоит в том, что вероятность возвращения в начало есть 4/16, и это число ввиду независимости компонент блуждания есть произведение P(X = 0) на P(Y = 0). Это допускает следующую интерпретацию. После двух шагов 25 % частиц в среднем вернется в начало. Вклад в среднее число возвращений в начало координат будет тогда равен 4/16•1 + 12/16•0 = 4/16. Вычислим вероятность того, что частица попадет в начало после 2, 4, 6, ... шагов, и, сложив все эти значения, найдем математическое ожидание числа возвращений частицы в начало.
После 2n шагов, n = 1, 2, ..., вероятность того, что частица
вернулась в начало координат, равняется
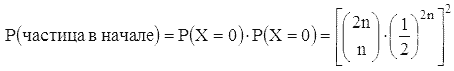
так как для осуществления этого события мы должны иметь
равные количества шагов как по вертикали, так и по горизонтали. (Напомним, что
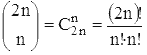 -
количество сочетаний из 2n элементов по n.) Строго говоря, надо было бы
поставить индексы у X и Y и писать X2n и т.д., но это выглядит
неприятно и отпугивающе. Просуммируем теперь приближенные выражения для этих
вероятностей и найдем математическое ожидание числа возвращений. Для больших
значений n можно применить формулу Стирлинга, приведенную в задаче
"Равновесие при бросании монет", и получить
-
количество сочетаний из 2n элементов по n.) Строго говоря, надо было бы
поставить индексы у X и Y и писать X2n и т.д., но это выглядит
неприятно и отпугивающе. Просуммируем теперь приближенные выражения для этих
вероятностей и найдем математическое ожидание числа возвращений. Для больших
значений n можно применить формулу Стирлинга, приведенную в задаче
"Равновесие при бросании монет", и получить
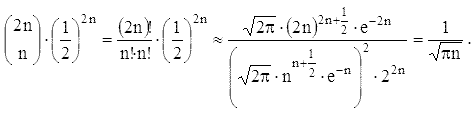
Тогда для больших n имеем
![]()
Эти вероятности надо просуммировать по n. Из задачи
"Выбор
купонов" известно, что
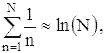
и последнее выражение неограниченно растет с возрастанием N.
Найдем вероятность того, что частица вернется в начало после числа шагов,
равного 2, 4, 6, 8, , .., 2n. Каждая из этих вероятностей есть также среднее
значение числа случаев, когда частица попадает в начало после ровно 2n шагов.
Чтобы получить общее математическое ожидание числа возвращений частицы в начало,
просуммируем эти значения, пользуясь тем фактом, что сумма средних есть среднее
суммы. Видим, что среднее число возвращений в начало бесконечно, и вероятность
возвращения в начало P = 1. Таким образом, частица не только вернется, но будет
возвращаться бесконечное число раз. Более точно, надо сказать, что почти каждая
частица возвращается бесконечно часто, так как существуют пути такие, например
как постоянное направление на северо-восток, которые позволяют некоторым
частицам уходить в бесконечность. Но доля таких частиц равна нулю.
Публикуется по работе: Пятьдесят занимательных вероятностных задач с решениями. Ф.Мостеллер, перев. с англ., издание второе. М. Наука, 1975, 112 с.
Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката
Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"
Редактор сайта: Гунькин И.А. (termist.com@gmail.com)