Термист Термомеханическое упрочнение арматурного проката технология, средства, разработка

Статистическая оценка

Статистическая оценка - некоторая функция от результатов наблюдений, предназначенная для статистического оценивания неизвестных характеристик и параметров распределения вероятностей. Выделяется случай, когда распределение вероятностей принадлежит какому-либо известному семейству, зависящему от конечного числа параметров. О методах непосредственной С. о. функциональных характеристик распределения вероятностей, например, неизвестной функции распределения или его плотности, см. "Непараметрические методы математической статистики". Напр., если результаты наблюдений X₁, ..., X_n - независимые случайные величины, имеющие одно и то же нормальное распределение с неизвестным математическим ожиданием a, то выборочное среднее - среднее арифметическое результатов наблюдений -
,
и выборочная медиана
Me_набл = x_(m), где m=(n+1)/2 при нечетном n,
Me_набл = (x_(m)+x_(m+1))/2, где m=n/2 при четном n,
где X_(m) - элементы вариационного ряда, соответствующего результатам наблюдений X₁, ..., X_n, являются С. о. неизвестного параметра a. Такие С. о., приводящие в конкретном случае к числовому значению параметра, называются точечными.

В дальнейшем рассматриваются лишь точечные статистические оценки. О С. о., выраженных целым множеством значений, см. в ст. "Интервальная статистическая оценка". В качестве С. о. какого либо параметра Θ распределения вероятностей естественно выбирать такую функцию Θ_n(X₁, ..., X_n) от результатов наблюдений X₁, ..., X_n, которая в некотором определённом смысле близка к истинному значению параметра. Принимая какую-либо меру «близости» С. о. к значению оцениваемого параметра, можно сравнивать различные оценки. Обычно мерой близости С. о. к истинному значению параметра служит величина среднего значения квадрата ошибки
Ε_Θ(Θ^*_n - Θ)² = D_ΘΘ^*_n + (Θ - Ε_ΘΘ^*_n)²
(выражающаяся через математическое ожидание оценки Ε_ΘΘ^*_n и её дисперсию D_ΘΘ^*_n, вычисленные по распределению, зависящему от неизвестного значения Θ). В классе всех несмещённых оценок Θ^*_n (для которых Ε_ΘΘ^*_n ≡ Θ при всех Θ) наилучшими с этой точки зрения будут статистические оценки, имеющие при заданном n минимальную возможную дисперсию при всех Θ (такие С. о. наз. также эффективными). Указанная выше С. о. X_{ср_n} для параметра a нормального распределения является наилучшей несмещённой оценкой, поскольку дисперсия любой другой несмещённой С. о. параметра a^* удовлетворяет неравенству D_aa^* ≥ D_aX_{ср_n} = σ²/n, где σ² - дисперсия исходного нормального распределения. В конкретных случаях отыскание наилучших статистических оценок облегчается с помощью достаточных статистик, так как наилучшую несмещённую оценку нужно искать в классе С. о., зависящих только от достаточной статистики. Имея в виду построение С. о. для больших значений n, изучают также асимптотические свойства С. о. Естественно, например, предполагать, что вероятность отклонений Θ^*_n от истинного значения параметра Θ, превосходящих какое-либо заданное число, будет стремиться к нулю при n → ∞. Статистические оценки с таким свойством называются состоятельными оценками. Несмещённые С. о., дисперсия которых стремится к нулю при n → ∞, являются состоятельными. Асимптотическое сравнение С. о. производят по отношению их асимптотических дисперсий. Так, среднее арифметическое X_{ср_n} в приведённом выше примере наилучшая и, следовательно, асимптотически наилучшая С. о. для параметра a, тогда как выборочная медиана µ_n, являющаяся также несмещённой оценкой, не является асимптотически наилучшей, так как

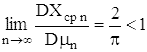
(тем не менее, использование µ_n имеет свои положительные стороны; например, если истинное распределение не является в точности нормальным, а несколько отличается от него, то дисперсия X_ср n может резко возрасти, а дисперсия µ_n остаётся почти той же, то есть µ обладает свойством, называемым прочностью или робастностью).

Одним из распространённых общих методов получения статистических оценок параметров распределения является метод моментов, который заключается в приравнивании определённого числа выборочных моментов соответствующим моментам исходного распределения, которые суть функции от неизвестных параметров, и решении полученных уравнений относительно этих параметров. Хотя метод моментов часто удобен в практическом отношении, однако С. о., найденные при его использовании, вообще говоря, не являются асимптотически наилучшими. Более важным с теоретической точки зрения представляется метод максимального правдоподобия, который приводит к оценкам, являющимся при некоторых общих условиях асимптотически наилучшими. Близок к последнему методу и метод наименьших квадратов.

Теория точечных статистических оценок не даёт возможности сделать заключение о "точности" таких оценок. В этом отношении С. о. неизвестных параметров существенно дополняются результатами интервального оценивания с помощью доверительных интервалов.

Статистическая оценка является вариантом более общего понятия статистического решения (см. Теория статистических решений). В рамках этого понятия рассматриваются бейесовские и минимаксные С. о.

Опубликовано по материалам: Математический энциклопедический словарь. / Гл. ред. Ю.В.Прохоров; Ред. кол.: С.И.Адян, Н.С.Бахвалов, В.И.Битюцков и др. - М.: Сов. энциклопедия, 1988. - 847 с. стр. 559 - 560.

К началу страницы

Web-сайт “Термист” (termist.com)
Термомеханическое упрочнение арматурного проката

Отсутствие ссылки на использованный материал является нарушением заповеди "Не укради"

Редактор сайта: Гунькин И.А. (termist.com@gmail.com)